Sistemas de equações: resolução algébrica e gráfica

René Descartes, ao inventar o plano cartesiano, reuniu a Aritmética, a Álgebra e a Geometria em um só contexto e nos ofereceu um novo sentido a Matemática. A possibilidade de transformar equações do 1º grau, com 2 variáveis, em gráficos e vice-versa nos mostra formas distintas para se confirmar a solução de um problema. Hoje, principalmente como professores de Matemática, sabemos da importância em apresentar aos nossos alunos diferentes caminhos para solucionar um problema e isso ajuda a maioria dos estudantes a compreender melhor as ideias envolvidas. Para entendermos melhor, vamos encontrar os valores de x e y que satisfazem, ao mesmo tempo, as equações do sistema abaixo utilizando tabelas, através do método da substituição e também do método da adição e em seguida vamos representar a solução gráfica. Usando tabelas:
Fazendo as devidas transformações algébricas obtemos o sistema equivalente:

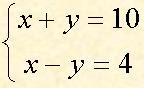E montamos uma tabela para cada equação com algumas das soluções. A solução comum é a solução do sistema. 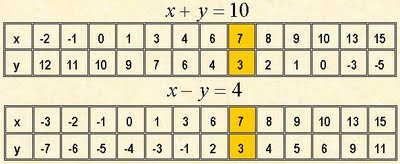Portanto o par de números x = 7 e y = 3 é a solução do sistema.

O método da substituição:
A partir do sistema equivalente temos:

substituindo na 2ª equação o valor de x por 10 - y temos

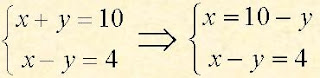
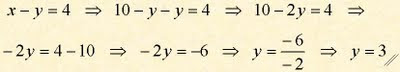para encontrar o valor de x fazemos:
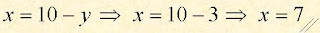Obtivemos outra vez os valores x = 7 e y = 3

O método da adição:
Novamente a partir do sistema equivalente, adicionamos* membro a membro os termos

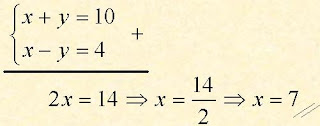Agora consideramos a equação que você achar mais simples no sistema para achar y:

A solução gráfica:
A partir dos pares indicados na tabela podemos marcar os pontos no plano cartesiano e obter as duas retas. O ponto de intersecção entre as duas retas é a solução do sistema.

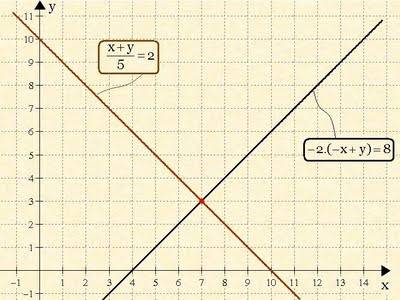Portanto o par de números ( 7 , 3 ) é de fato a solução do sistema.

Para finalizar podemos perceber que, de modo geral, num sistema formado por duas equações do 1º grau com duas variáveis pode ocorrer:
a) uma única solução: graficamente teremos duas retas concorrentes;
b) nenhuma solução: graficamente teremos duas retas paralelas;
c) infinitas soluções: graficamente teremos duas retas coincidentes.
_______________
*A adição só se faz conveniente quando anula o coeficiente de uma das incógnitas, caso contrário multiplica-se por um fator os termos de uma das equações de forma a tornar conveniente e anular um dos coeficientes das incógnitas.