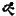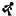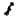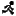 , que ilustra bem o fato. Finalizando, esse povo que faz Matemática tem imaginação e criatividade né? Até o próximo.
, que ilustra bem o fato. Finalizando, esse povo que faz Matemática tem imaginação e criatividade né? Até o próximo.quinta-feira, 30 de julho de 2015
A área do círculo e a imaginação dos matemáticos
O conceito de área de figuras planas cuja superfície a ser medida é limitada por segmentos de reta no ensino fundamental não é algo que estudantes encontram grandes dificuldades. De forma geral os livros que temos exploram bem o assunto. Já no caso de área de figuras planas cujo contorno não é formado por segmentos de reta (como por exemplo, o círculo ou parte dele, entre outras) é um problema. Sinto falta de situações mais adequadas e criativas (inclusive em avaliações oficiais) e acredito que poderia ser melhor explorado ou problematizado. Problemas envolvendo a área do círculo são boas oportunidades de contexto dentro da própria Matemática. Observe a figura a seguir:
No quadrado de lado unitário, qual é a área do olho (região amarela)?
Nesta próxima figura temos um círculo entre dois quadrados. Veja:
O quadrado maior possui área de 36 cm² e menor área de 25 cm². Entre os dois quadrados temos um círculo e isso nos garante que a área do círculo, em destaque, é maior que 25 cm² e menor que 36 cm², más não conseguimos definir exatamente esse valor. E como descobrir?
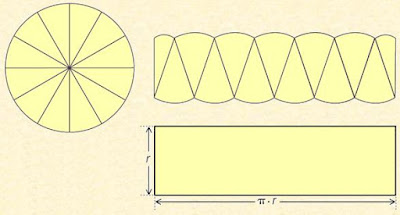
Esse é um problema ocupou parte da mente de vários matemáticos gregos; entre eles, podemos citar Eudoxio e Arquimedes. Ambos construíram um método para calcular áreas de figuras planas, que consiste na aproximação por polígonos. A ideia de aproximação não fornece um valor exato, a menos que imaginemos uma seqüência infinita de aproximações. Imaginar o círculo “cortado” em formato de pizza como ilustra a figura abaixo é o começo desse método. Imaginar ainda que esses pedaços possam ser infinitamente menores pode nos fornecer uma expressão que nos dará a área do círculo com base em algo já conhecido.
Observando as figuras é possível concluirmos que a área do círculo é a mesma área de um retângulo de base πr e altura r, ou seja, A = πr². Como sugestão veja este link:  , que ilustra bem o fato. Finalizando, esse povo que faz Matemática tem imaginação e criatividade né? Até o próximo.
, que ilustra bem o fato. Finalizando, esse povo que faz Matemática tem imaginação e criatividade né? Até o próximo.
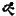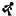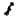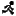 , que ilustra bem o fato. Finalizando, esse povo que faz Matemática tem imaginação e criatividade né? Até o próximo.
, que ilustra bem o fato. Finalizando, esse povo que faz Matemática tem imaginação e criatividade né? Até o próximo.
Assinar:
Postar comentários (Atom)

*O Portal da Matemática OBMEP oferece gratuitamente, a todos os estudantes do país, materiais didáticos de qualidade relacionados à grade curricular do 6º ano do Ensino Fundamental ao 3º ano do Ensino Médio. Já utilizamos e incentivamos nossos estudantes a utilizarem, cada vez mais esses materiais. Complemente e aprofunde seus estudos com videoaulas, exercícios resolvidos, caderno de exercícios, material teórico e aplicativos iterativos. Aproveite!!
* Aproveite e conheça nossa história na OBMEP.
▼ Reflita | Uma pausa, um pensamento
![]()
▼ Por onde andei(o) enquanto... ♫ | Link's
▼ Seções do Blogue | Acesso Rápido ★





































































Nenhum comentário:
Postar um comentário
►ATENÇÃO - Leia a política para comentários na página de contato.
Observação: somente um membro deste blog pode postar um comentário.