O tal do M.M.C. ... e algumas idéias relacionadas

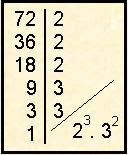
Outro dia desses fiz a decomposição do número 72 no quadro para uma turma do 1º ano do ensino médio e pasmem (eu tô até hoje!!!), vários alunos disseram que estava fazendo o m.m.c. ( putz grilo de novo!!!! ). Bom ... ou melhor mau, por esse motivo resolvi postar aqui uma retomada deste conceito.
Inicialmente vamos relembrar o conceito de múltiplo. Se multiplicarmos o número 6 por cada um dos números da seqüência dos naturais:
6 x 0 = 0 ; 6 x 1 = 6 ; 6 x 2 = 12 ; 6 x 3 = 18 ; 6 x 4 = 24 ; 6 x 5 = 30 e assim por diante os resultados obtidos são os múltiplos do número 6 e podem ser representados da seguinte forma:

M(6) = {0 , 6 , 12 , 18 , 24 , 30 , 36 , ...}.

Observe que o conjunto de múltiplos de um número é infinito; que todo número é múltiplo de si mesmo e que o menor múltiplo de um número é sempre o zero.

Assim: “Múltiplo de um número é o produto desse número por um número natural qualquer”

Observe, por exemplo, que quando afirmamos: 48 é divisível por 3 é o mesmo que dizer que 48 é múltiplo de 3. Perceba que 48 também é múltiplo de 0, 1, 2, 4, 6, 8, 12, 24 e 48. Ok?

Mínimo Múltiplo Comum ou simplesmente M.M.C.

Dois, três ou mais números sempre têm múltiplos comuns a eles. Vamos achar os múltiplos comuns de 6 e 8:

M(6) = {0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, ...}.
M(8) = {0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, ...}.

Percebemos que os múltiplos comuns de 6 e 8 são: 0, 24, 48, 72, 96, ...
Dentre estes múltiplos, diferentes de zero, 24 é o menor deles. Chamamos o 24 de mínimo múltiplo comum de 6 e 8, ou seja, m.m.c.(6; 8) = 24

Assim: “Dados dois ou mais números, mínimo múltiplo comum é o menor número, diferente de zero, que é múltiplo simultaneamente dos números dados”.

Cálculo do M.M.C.

Podemos calcular o m.m.c. de dois ou mais números utilizando a fatoração.
Acompanhe o cálculo do m.m.c. de 12 e 40:

1º) decompomos os números em fatores primos
2º) o m.m.c. é o produto dos fatores primos comuns e não-comuns:

12 = 2 x 2 x 3 = 2² . 3
40 = 2 x 2 x 2 x 5 = 2³ x 5
m.m.c(12; 40 ) = 2 x 2 x 2 x 3 x 5 = 120

Assim: “O m.m.c. de dois ou mais números, quando fatorados, é o produto dos fatores comuns e não-comuns a eles, cada um elevado ao maior expoente”

Processo prático ou decomposição simultânea para encontrar o M.M.C.

Neste processo decompomos todos os números ao mesmo tempo, num esquema como mostra a figura ao lado. O produto dos fatores primos que obtemos nessa decomposição é o m.m.c. desses números. Ao lado vemos o cálculo do m.m.c.(15, 24, 60). Portanto,

m.m.c.(15, 24, 60) = 2 x 2 x 2 x 3 x 5 = 120

Propriedades do M.M.C.

Entre os números 3, 6 e 30, o número 30 é múltiplo dos outros dois. Neste caso, 30 é o m.m.c. de 3, 6 e 30. Ou seja: m.m.c. (3, 6, 30) = 2 x 3 x 5 = 30

“Dados dois ou mais números, se um deles é múltiplo de todos os outros, então ele é o m.m.c. dos números dados.”

Considerando os números 4 e 15, que são primos entre si. O m.m.c. de 4 e 15 é igual a 60, que é o produto de 4 por 15. Ou seja: m.m.c.(4,15) = 2 x 2 x 3 x 5 = 60

“Dados dois números primos entre si, o m.m.c. deles é o produto desses números.”

Agora que revimos o conceito de M.M.C. na aritmética que tal você pesquisar um pouco mais e descobrir e aprofundar como se encontra o M.M.C. de expressões algébricas como 12a²b e 15ab³ ou expressões do tipo 2x² + 4xy + 2y² e 6x + 6y ?

Responde essa:

Um médico prescreve três medicamentos: A(de 3 em 3 horas) , B(de 4 em 4 horas) e C(de 6 em 6 horas) para um de seus pacientes. Se o paciente ingeriu os medicamentos todos juntos às 7 h da manhã, que horas voltará a ingerir todos juntos novamente?